Two Particles with Equal Charges (X and Y) – The Two particles, X and Y, having equal charges subsequently accelerating, finished the same possible difference, enter a section of the uniform magnetic field, and describe a circular path of radii ‘r1 and ‘r2’, respectively. The fraction of the mass of X to that of Y is –
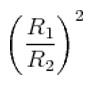
Table of Contents
Solution –
The correct possibility is –
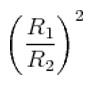
r=√2mk/qB = 1/B√2m/Vq ⇒ r ∝ √m ⇒ m1/m2=(R1/R2)2
Explanation of Two Particles with Equal Charges (X and Y)
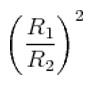
Particles X and Y of respective masses m₁ and m₂ are carrying charge q describing circular paths with respective radii R1 and R2 such that:
R1 = m1V1/qB
R2 = m2V2/qB
Since both particles accelerate through the same potential difference, both will have the same
kinetic energy.
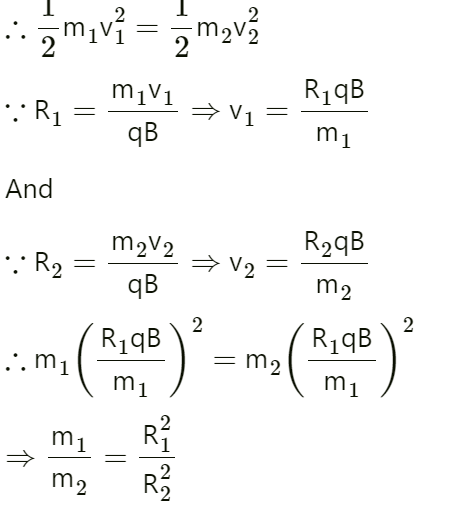
Some Similar Questions Related to Two Particles with Equal Charges (X and Y)
- After being accelerated by the same potential difference, two particles, A and B, having equal charges +6 C, enter a region of uniform magnetic field and describe circular paths of radii 2cm and 3cm, respectively. The ratio of the mass of A to that of B is:
Solution –
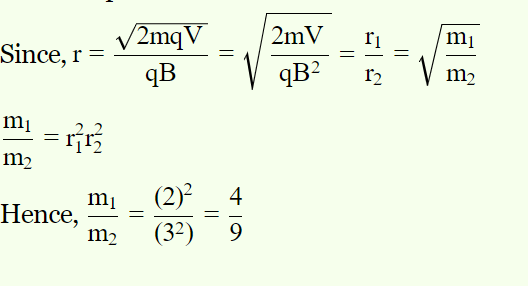
A positively charged particle affecting due east enters an area of uniform magnetic field directed vertically upwards. This particle will:
Solution –
When a positively charged enters a region of uniform magnetic field directed vertically upwards, it experiences a centripetal force that moves the particle in a circular path with a constant speed (in a clockwise direction).
- An electron moving with speed along the positive x−axis at y=0 enters a region of the uniform magnetic field to the right of the y−axis. The electron exits from the area after some time with the speed v at coordinate y, then :
Solution –
![]()
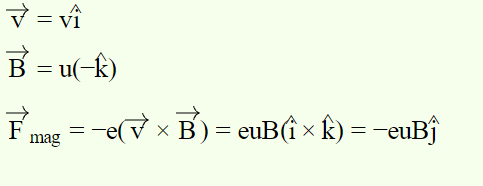
Thus the electron gets deflected towards the −ve y−axis.
Since no work is done during motion in a magnetic field, the electron’s speed will remain constant.
- A proton and alpha particle enter a uniform magnetic field B region, moving at right angles to field B. If the radius of circular orbits for both the particles is equal and the kinetic energy acquired by the proton is 1 MeV, the point obtained by the alpha particle will be:
Solution –
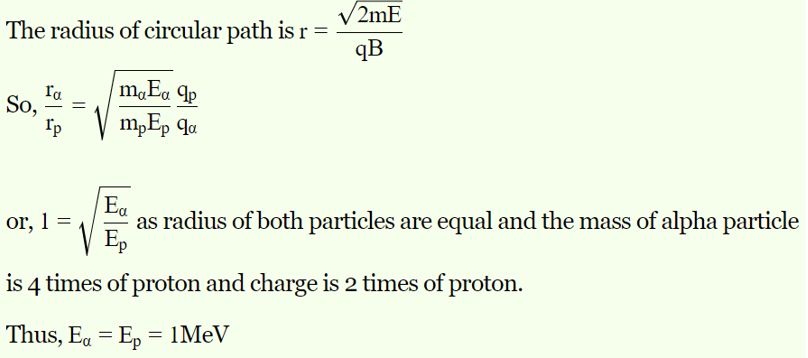
- Two particles, A and B, having equal charges after being accelerate by the same potential difference, enter a region of the uniform magnetic field. The particles describe circular paths of radii R1 and R2, respectively. The ratio of the masses of A and B is.
Solution –
![]()

Coulomb’s Law
Coulomb’s Law stretches the force of attraction or repulsion between two point charges. Uncertainty two point controls q1 and q2 detached by a distance r formerly the magnitude of the strength of attraction or repulsion between them is –
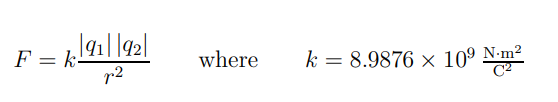
It is the magnitude of the force which each charge exerts on the other direction (recall Newton’s Third Law). The symbol k, as used here, involves electrical points. It has nothing to do with any Boltzmann’s constant or spring constants!
Uncertainty the charges q1 and q2 are of the same sign (positive or negative) the force is mutually repulsive, and the emphasis on each direction points away from the other charge.
Suppose the charges are of opposite signs (one optimistic, one negative), then the force is mutually attractive, and the emphasis on each direction points toward the other.
The constant k in Eq. 1.3 is often written as –
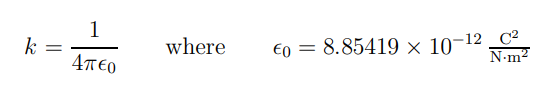
WORKED EXAMPLES

For historical reasons but also because, in later applications, the constant is more convenient and is called the permittivity constant.
When several points charges are present. The total force on a particular order q0 is the vector sum of the individual troops got from Coulomb’s Law. (Thus, electric forces have a superposition property.)
For a continuous charge distribution, we need to divide the charge distribution into tiny pieces and add up the individual forces with integrals to get the net force.
Orbital Wave Function
The wave functions for s states are functions of r and do not show any dependence on angular coordinates.
Therefore, the orbitals represented by the wave functions are spherically symmetric. Consequently, the probability of finding the electron at a given distance from the nucleus in such an orbital is equal in all directions.
